把m个小球放入n个不同的盒子，一般用“隔板法”求解。“有趣的数学（http://www.mathsisfun.com/ ）”给出了另外一种非常有意思的解法。
假设现在有3个完全相同的球要放入5个不同的盒子（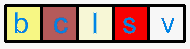
）中，应该有多少种分配方案呢？
先来看看其中一种分配方案，在C盒中放入所有的3个小球。这一分配方案我们是通过以下步骤来实现的：我们先来到b，因为我们不在这里放球，所以跳过（用→表示）；经过C盒时我们放3个小球，用○○○表示；接下来经过l,S,V时都不放小球，因此仍然用→表示。整个执行的过程如
。
再来看另外一种方案，这回我们要在b, l, v盒中分别放一个小球，这样按照上面的方法，整个过程如
。
其它方案等等。。。
这样其实我们就将3个相同的小球放入5个不同盒子里的问题简化为，在（5+3-1）个位置选出3个位置画圈。因此分配方案的种数为C(5+3-1,3)=35。
所以一般的，把m个完全相同的小球放入n个不同的盒中，其分配方案有：C(m+n-1,m)种。
[注]：本文译改（By 水南）自：http://www.mathsisfun.com/combinatorics/combinations-permutations.html
回复Comments
作者:
{commentrecontent}