Veteran's Blog

非原创作品，原文看这里

在计算机图形的许多效果中，水纹效果能够更多地吸引人注意。他模拟的是水被扰动后的运动。

这篇文章包含两个部分，第一部分讲了水的运动如何杯模拟。第二部分讲了当遇到一个透明的表面以后如何计算光的折射。利用这些知识你可以制作出更加吸引人的动画。

第一个部分：如何模拟波形

这一效果背后的运行机制也是非常简单的，我相信它是在对区域取样的测试中被意外发现的。在我们研究波形模拟的计算之前，来看一下什么是区域取样。

区域取样

区域取样在计算机的图形学中是一个普通的运算法则。已知一个二维的空间，(x,y)的值受到了来自他周围的位置的影响，例如（x+1,y）(x-1,y)(x,y+1)和（x,y-1）。我们的波形模拟实际在一个三维的空间中，稍后再说这些东西。

区域取样例子：简单模糊

模糊一块地图是很简单的，你需要两个地图，一个包含你想要模糊的数据，一个用来存储结果。

运算的法则如下：（需要用到5个取样值）

ResultMap[x, y] := ( SourceMap[x, y] +

                     SourceMap[x+1, y] +

                     SourceMap[x-1, y] +

                     SourceMap[x, y+1] +

                     SourceMap[x, y-1] ) DIV 5

（x,y）的值是它周围的值得平均值。当然，当你想模糊图像的时候，事情也许会变得复杂一些，但是你已经有了这样的想法。

创建一个波形的模拟基本上和这个相同的，但是（x,y）的计算是以一种不同的方式来计算的。先前我谈到过波形是在三维空间中的，那第3维就是时间。（晕！我以为是深度）；换句话说：当计算波形时候，我们必须知道波形如何看上去像持续了一段时间。在下一帧中，结果图像变成了源图像。

这是一个真实的波形模拟运算法则

ResultMap[x, y] := (( CurrentSourceMap[x+1, y] +

                      CurrentSourceMap[x-1, y] +

                      CurrentSourceMap[x, y+1] +

                      CurrentSourceMap[x, y-1] ) DIV 2 ) - 

                      PreviousResultMap[x, y]

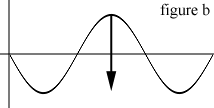
你能够看到开始的四个值是从当前的原图像中获得的，并且被分割为二。这个结果是平均值的两倍。接下来，我们减去我们正在操作的上一个地图的(x,y)的值。这样产生出了一个新值。图表1和图表2展示了波形的效果。

水平的灰线表示波形的平均高度。如果上一个的(x,y)比平均值低，波形将会下降到平均水平以下。

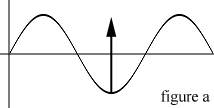
如果上一个的（x,y）比平均值高，波形会高出平均水平。

衰减

每次波形上下移动，他的能量就会分布到一个增长的区域中。这就意味着波形的振幅会逐渐的下降。使用一个阻尼运动来模拟这些，这个因子就是振幅的百分数或者数量级，从当前的振幅中减去让高振幅逐渐消失的更快和，而低振幅消失的更慢。在以下的例子中，每次移动都会从中减去1/16的振幅。

波形模拟的例子

以下的代码段包含有一些汇编程序，但是我已经用Pascal替换掉了，以便你能够更简单的进行移植到其他的平台。

const

  MAXX = 320;                 { Width and height of WaveMap }

  MAXY = 240;

  DAMP = 16;                  { Damping factor }

{ Define WaveMap[frame, x, y] and frame-indices }

var

  WaveMap: Array[0..1, 0..(MAXX-1), 0..(MAXY-1)] of SmallInt;

  CT, NW: SmallInt;

.

.

procedure UpdateWaveMap;

var

  x,y,n: Smallint;

begin

  { Skip the edges to allow area sampling }

  for y := 1 to MAXY-1 do begin

    for x := 1 to MAXX-1 do begin

      n := ( WaveMap[CT,x-1,y] +

             WaveMap[CT,x+1,y] +

             WaveMap[CT,x,y-1] +

             WaveMap[CT,x,y+1] ) div 2 -

             WaveMap[NW,x,y];

      n := n - (n div DAMP);

      WaveMap[NW,x,y] := n;

    end;

  end;

end;

.

.想要执行这些代码的话，需要给他的result一个图形。在第二部分中将会讲到这是什么。重要的是在你的重复中交换了source和result的值。

Temporary_Value := CT;

CT := NW;

NW := Temporary_Value;

但是，CT和NW的意思是什么呢？CT和NW是不同的波形地图中的点。CT指的是当前的地图，他包含我们需要产生的新的波形地图的数据，依靠的是NW点。CT和NW能够存储两个值，1和0。但是决不会相同。因为我们在每次循环都进行了交换，新的波形地图包含的是当前的波形地图产生之前的地图。我觉得这只是听上去很复杂。

让他移动

以上的程序只是波形的简单处理，但是，我们如何让整个都移动呢？一个没有扰动的波形地图包含的全是0。要想创建一个波形，只要给出一个随机的位置，像以下这样来改变数值。

WaveMap[x, y] := -100;

更高的值，意味着更大的波形

更多文章看www.toswf.com